In the last months and years, I have stumbled upon many papers about quantum computing and some of the I have also read, some of them were just to Noble-prizy for me. Some were about the topology of quantum computers, some were about specific algorithms like Shor’s algorithm, some were about having fun with quantum computing, and some about physics (like Landauers Irreversibility and Heat Generation in the Computing Process or Benett’s Logical Reversibility of Computation).

But this one is interesting, since it defines the very basic properties of a quantum computer, or more specifically about the qubits needed for quantum computation. The discussed paper titled The Physical Implementation of Quantum Computation is from 2008 and was published by David P. DiVencenzo.

After a short intro of the state of the art (remember, it’s from 2008!), he described the five properties a quantum computer must have. Now these seem to be obvious to most readers, but I think that it is worth to reiterate them again.

1. A scalable physical system with well characterized qubits

Yes, this maybe be an obvious one. First, you need some qubits.

For a start, a physical system containing a collection of qubits is needed.

And these qubits must behave in a certain way and includes the idea of the property of superposition.

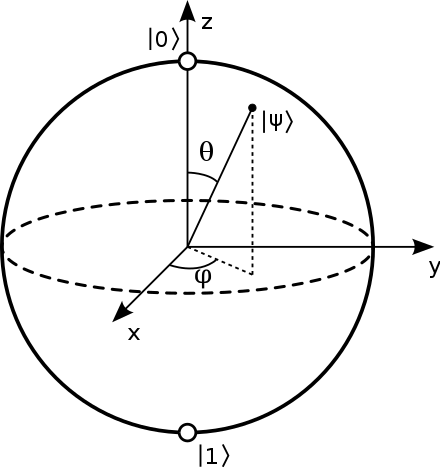
The generic notation for a qubit state denotes one state as |0⟩ and the other as |1⟩. The essential feature that distinguishes a qubit from a bit is that, according to the laws of quantum mechanics, the permitted states of a single qubit fills up a two-dimensional complex vector space.

Single bits only support a 1 or 0, on or off, true or false. Qubits not only have the simple binary state, they have values from 1 to 0 in a two-dimensional state which is often visualized as a bloch sphere. Mathematically this is described as a “|Ѱ⟩ = a |0⟩ + b |1⟩” and the normalization “|a⟩^2 + |b⟩^2 = 1”.

Based on such a single qubit, more sophisticated combinations can be constructed. E.g. having a two-qubits-system that show the property of entanglement.

2. The ability to initialize the state of the qubits to a simple fiducial state, such as |000…⟩

For a programmer this is logical: you have to define the initial state of a system before a computation can start. Numbers are initialized to zero, strings are initialized to empty strings, or booleans are initialized to false. Depending on the programming language you use, you have to do it either explicitly or it happens implicitly.

And the same applies to quantum computer and its qubits. The qubits have to be initialized to a defined state, which is usually |0⟩.

This arises first from the straightforward computing requirement that registers should be initialized to a known value before the start of computation.

But differently to classical computers, quantum computers have some special properties. Quantum computers have, because of their way how they have been constructed and how they work, a higher error rate. Qubits can flip (bit-flip) or turn around (phase flip).

Classical computers have errors as well, but they are rare events. We are talking of rates of 10^-13 (or much better) for ECC memory and the detection/correction is already well understood. For quantum computers we have a much high error rate of 10^-4 per gate operation. So this brings us to another reason for correct initialization:

There is a second reason for this initialization requirement: quantum error correction (see requirement 3 below) requires a continuous, fresh supply of qubits in a low-entropy state (like the |0⟩ state).

3. Long relevant decoherence times, much longer than the gate operation time

“Decoherence can be viewed as the loss of information from a system into the environment” (from https://en.wikipedia.org/wiki/Quantum_decoherence) which basically means, that after some time you cannot “trust” the information stored in a qubit.

Decoherence times characterize the dynamics of a qubit (or any quantum system) in contact with its environment.

And the time it takes that a qubit “loses” the information is called the decoherence time. After some hundredths of microseconds or up to seconds (depending on the concrete physical implementation) the state changes unintentionally.

The (somewhat overly) simplified definition of this time is that it is the characteristic time for a generic qubit state |ψ⟩ = a|0⟩ + b|1⟩ to be transformed into the mixture ρ = |a|^2|0⟩⟨0|+|b|2^|1⟩⟨1|.

And…

For the same reason, decoherence is very dangerous for quantum computing, since if it acts for very long, the capability of the quantum computer will not be so different from that of a classical machine.

Decoherence is an unwanted side effect and limits the power of quantum computers. The longer the qubits can hold information, which is used in computation, the more operations a quantum computer can perform. Simplified spoken, the decoherence time defines the length of an algorithm and is one property to be improved. The longer, the better in this case.

The decoherence time must be long enough that the uniquely quantum features of this style of computation have a chance to come into play.

4. A “universal” set of quantum gates

Universal quantum computing, which is different to quantum annealing or adiabatic quantum computation, relies on gates. Classical computers operate with basic logical gates like AND, OR, NOT, XOR,… and many of them are combined to construct CPUs. Quantum computers use qubits and gates are used to construct circuits to solve a problem.

This requirement is of course at the heart of quantum computing. A quantum algorithm is typically specified as a sequence of unitary transformations U1, U2, U3,…, each acting on a small number of qubits, typically no more than three.

Unitary? Transformations? Sounds horrifying, doesn’t it? Don’t worry. Simplified said, gates (or quantum operations) modify the state of usually one or two qubit. In contrast to logical gates, quantum operations flip and rotate qubits (remember from the first point, qubits act on two-dimensional complex vector space) and a combination of such gates operating on qubits be used to construct a universal quantum computer.

This immediately poses a problem for a quantum computation specified with three-qubit unitary transformations; fortunately, of course, these can always be re-expressed in terms of sequences of one- and two-body interactions, and the two-body interactions can be of just one type, the “quantum XOR” or “cNOT”.

So, all in all no big difference. The only issue we have, that the operations are not perfect.

Quantum gates cannot be implemented perfectly; we must expect both systematic and random errors in the implementation of the necessary Hamiltonians.

These errors are introduced for each applied operation. A “flip around x” is not always a flip by exactly π around x; a “rotation by π/2 around y-axis” is not always a rotation by π/2 around x-axis. It could be exactly π/2 around x, 0.01*π around y and π around z. So slightly off a perfect rotation. But these random errors sum up and after many many operations applied, these imperfections can lead to errors and these errors have to be detected and corrected.

5. A qubit-specific measurement capability

If a tree falls in a forest and no one is around to hear it, does it make a sound? And similarly; if a qubit calculates in a quantum computer and no one is around to read it, does it calculate? 🤔 Reading it out is actually doing a measurement of the qubits state. This results in a value of 0 or 1.

Finally, the result of a computation must be read out, and this requires the ability to measure specific qubits.

The paper discusses another (theoretical🤔) measurement which makes the reuse of a qubit easier.

If the measurement is “non-demolition”, that is, if in addition to reporting outcome “0” the measurement leaves the qubit in state |0⟩⟨0|, then it can also be used for the state preparation of requirement 2; but requirement 2 can be fulfilled in other ways.

Finally, a very important property of the measurement process is discussed.

As a simple example, if the quantum efficiency is 90%, then, in the absence of any other imperfections, a computation with a single-bit output (a so-called “decision problem”, common in computer science) will have 90% reliability. If 97% reliability is needed, this can just be achieved by rerunning the calculation three times.

This is maybe the biggest differentiation between classical and quantum computers. Classical computers are deterministic, and the algorithms run as well (except for AI and such). So will get the same result for the same input. Repeatedly. No matter where, in Europe or on Jupiter.

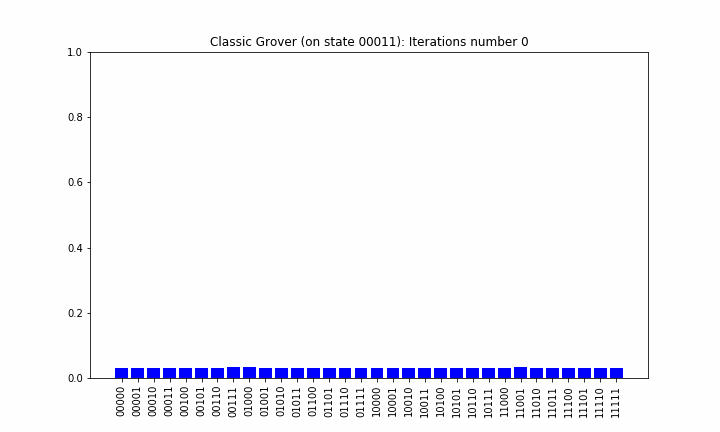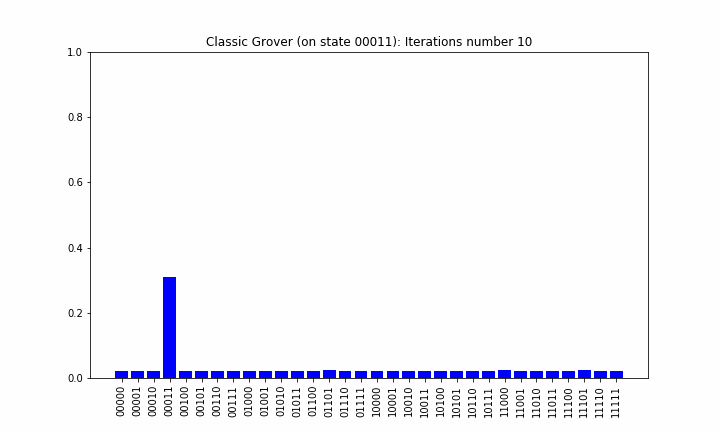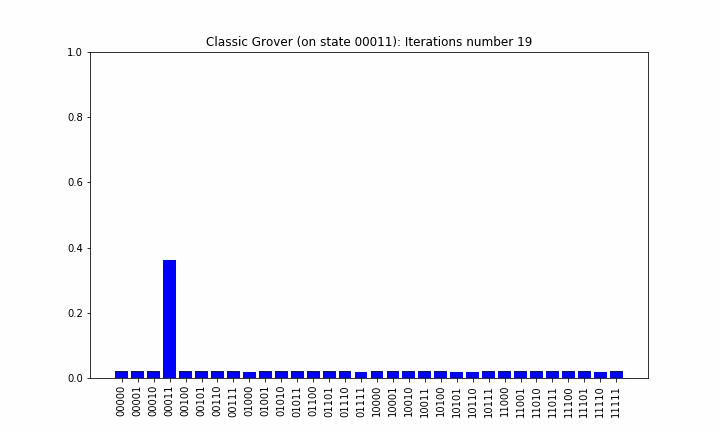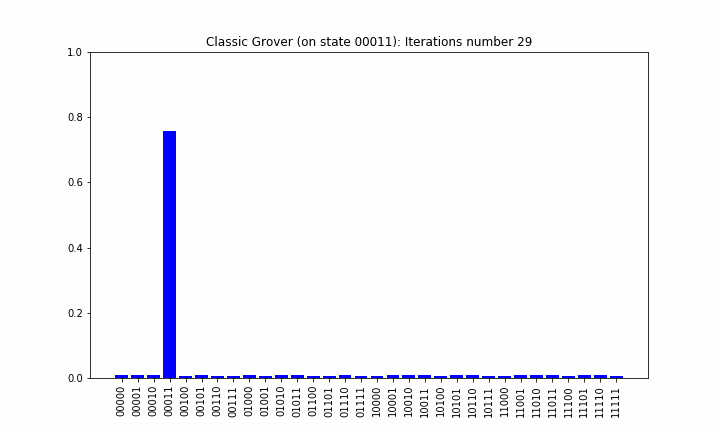
Quantum computers are probabilistic and running a circuit only once, returns one result. But the same input can lead to different outcome the next time. You run the circuits many time to increase the probability of a correct result. Some many thousand times. The distribution of the measurements is often visualized as a histogram. Interpretation is mostly up to the circuit designer if no obvious final result is achieved.

Conclusion

Five basic properties of qubits. All of them for each of seem to be simple. And you will agree that these are very basic but combined they have a very high impact. But the good thing is, current platforms are providing qubits as described and great frameworks like Google’s Cirq, Quiskit by IBM or C# by Microsoft hide some of this complexity. So, there we are. Ready can start to implement quantum circuits. But be aware, dragons ahead!

Sharing is caring!